Campus parking on Prime days only

Someone recently made a joke about we only being allowed to park a car on campus on prime days. This got me thinking, and since I need Matlab for school now, I thought I’d give ipython a test this time.

The joke was that you were only allowed to enter the campus with your car and make use of the parking space if the day was prime. They didn’t define prime days, so I guess I’ll define them as I please. Perhaps beginning the count in the year 0 (0 A.D.) and resetting it at some suitable time-frame. Whatever the count reset time-frame, the count will begin at 1 (sorry Dijkstra) and increment when the calendar day changes.

Let’s say we reset the count every year. We get up to 365, or 366 if we’re in a leap year. In this case this doesn’t really matter because 366 is even and so we can run our function with 365.

length(primes(365)) gives us 72. We would be able to park our car 72 times in a year. Not bad but from our knowledge of primes we have a hunch that resetting the count every month would yield better results (more parking, yay!). Lets check:

N = 100;
p = primes(N);
l = length(p);
primestep=zeros(1,N-1);
linear=2:N;

for i=linear
    primestep(i-1)=sum(p<=i);
end

plot(linear,primestep./linear,linear,1./log(linear),'r');
legend('Primes density','1/log(n)');
title(sprintf('Density of primes up to N=%d. versus 1/log(x)',N));

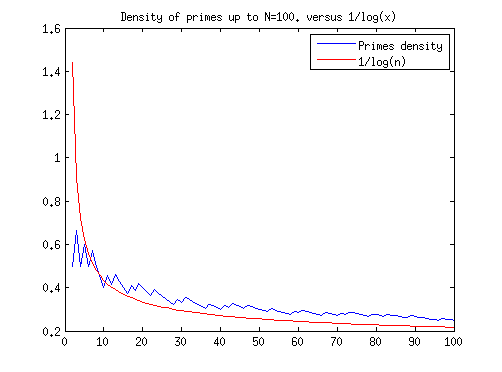
As we suspected, there is a clear benefit in resetting the count. The density of primes decreases logarithmically, and so we gain from resetting earlier rather than later. What’s a good (read, acceptable) time-frame though? Daily resets would make us very happy but they would also probably make management cry. Monthly resets sound like a good compromise.

By looking at our knuckles we check that there’s seven months with 31 days, which have a prime number more than the four existing 30 day months. With 10 primes in 30 days and 11 in 31, we amount to a total of 117 prime numbers when we add the months up. Lets keep February in mind though. February can have either 28 or 29 days, which means it can have either 9 or 10 prime days. Wrapping it up, we get either 126 or 127 prime days in a year by resetting the count monthly.

Settling with this monthly count we now realize not all days are equal. One shall not drive to school on a sunday as this is a day to sleep till lunch time, read a fine book and laugh at pictures of cats. There’s also the fact that the school year is decided by powerful forces which work in mysterious ways. Realizing this, let us confront our prime days with the school calendar.

This years calendar at my university is as follows:

• From September 17th till December 21st 2012
• From January 2nd till January 19th 2013
• From February 13th till March 27th 2013
• From April 2nd till June 15th 2013

With a full month having the prime distribution as:

>> primes(31)
ans =    2    3    5    7    11    13    17    19    23    29    31

We get four full months and six incomplete months. Here follows the usable prime days per month:

• September: 4
• October: 11
• November: 10
• December: 8
• January: 8
• February: 4 (2013 is not a leap year)
• March: 9
• April: 10
• May: 11
• June: 6

Totaling 81 days. Of those, we further need to deduct 12 prime sundays which gives as a final 69 days of campus parking. Having reached an acceptable number of parking days, I’ll stop. For now.

PS: I walk to school.